5. Setting up particles¶
5.1. Overview of the relevant Python classes¶
For understanding this chapter, it is helpful to be aware of the Python classes provided by ESPResSo to interact with particles:
ParticleHandleprovides access to a single particle in the simulation.ParticleListprovides access to all particles in the simulationParticleSliceprovides access to a subset of particles in the simulation identified by a list of ids or an instance ofsliceorrange.
In almost no case have these classes to be instantiated explicitly by the user.
Rather, access is provided via the system part attribute.
The details are explained in the following sections.
5.2. Adding particles¶
In order to add particles to the system, call
ParticleList.add():
import espressomd
system = espressomd.System(box_l=[10., 10., 10.])
p = system.part.add(pos=[1., 1., 1.], type=0)
This command adds a single particle to the system with properties given
as arguments, and it returns an instance of
ParticleHandle, which will be used to access
properties of the newly created particle. The pos property is required, all
other properties are optional.
All available particle properties are members of ParticleHandle.
Note that the instances of ParticleHandle returned by
ParticleList.add() are handles for the live particles in the
simulation, rather than offline copies. Changing their properties will affect the simulation.
It is also possible to add several particles at once:
import numpy as np
new_parts = system.part.add(pos=np.random.random((10, 3)) * box_length)
If several particles are added at once, an instance of
ParticleSlice is returned.
Particles are identified via their id property. A unique id is given to them
automatically. Alternatively, you can assign an id manually when adding them to the system:
system.part.add(pos=[1., 2., 3.], id=system.part.highest_particle_id + 1)
The id provides an alternative way to access particles in the system. To
retrieve the handle of the particle with id 5, call:
p = system.part.by_id(5)
5.3. Accessing particle properties¶
Particle properties can be accessed like any class member.
For example, to print the particle’s current position, call:
print(p.pos)
5.4. Modifying particle properties¶
Similarly, the position can be set:
p.pos = [1., 2.5, 3.]
Not all properties are writeable. For example, properties that are automatically derived from other properties are read-only attributes.
Please note that changing a particle property will not affect the ghost
particles until after the next integration loop. This can be an issue for
certain methods like espressomd.system.System.distance() which use
the old ghost information, while other methods like particle-based analysis
tools and espressomd.cell_system.CellSystem.get_neighbors() update the
ghost information before calculating the observable.
5.4.1. Vectorial properties¶
For vectorial particle properties, component-wise manipulation like
p.pos[0] = 1 or in-place operators like += or *=
are not allowed and raise an exception.
This behavior is inherited, so the same applies to pos after
pos = p.pos. If you want to use a vectorial property for further
calculations, you should explicitly make a copy e.g. via
pos = numpy.copy(p.pos).
5.5. Deleting particles¶
Particles can be easily deleted in Python using particle ids or ranges of particle ids. For example, to delete all particles of type 1, run:
system.part.select(type=1).remove()
To delete all particles, use:
system.part.clear()
5.6. Iterating over particles and pairs of particles¶
You can iterate over all particles or over a subset of particles (see Interacting with groups of particles) as follows:
for p in system.part:
print(p.pos)
for p in system.part.select(type=1):
print(p.pos)
You can iterate over all pairs of particles using:
for pair in system.part.pairs():
print(pair[0].id, pair[1].id)
5.7. Exclusions¶
Particles can have an exclusion list of all other particles where non-bonded interactions are ignored. This is typically used in atomistic simulations, where nearest and next nearest neighbor interactions along a chain of bonded particles have to be omitted since they are included in the bonding potentials. Exclusions do not apply to the short range part of electrostatics and magnetostatics methods, e.g. to P3M.
To create exclusions for particles pairs 0 and 1:
system.part.by_id(0).add_exclusion(1)
To delete the exclusion:
system.part.by_id(0).delete_exclusion(1)
The current list of exclusions is accessible in the
exclusions property.
5.8. Rotational degrees of freedom and particle anisotropy¶
When the feature ROTATION is compiled in, particles not only have a position,
but also an orientation that changes with an angular velocity.
A torque on a particle leads to a change in angular velocity depending on the
particles rotational inertia.
The property rinertia has to
be specified as the three eigenvalues of the particles rotational inertia tensor.
Even if the particle rotational inertia is isotropic, the rotation state can be
important if, e.g., the particle carries a dipole or is an active particle.
The rotational degrees of freedom are integrated using a velocity Verlet scheme. The implementation is based on a quaternion representation of the particle orientation and described in [Omelyan, 1998] with quaternion components indexing made according to the formalism \(q = a + b\mathbf{i} + c\mathbf{j} + d\mathbf{k}\) [Allen and Tildesley, 2017].
When the Langevin thermostat is enabled, the rotational degrees of freedom are also thermalized.
Whether or not rotational degrees of freedom are propagated,
is controlled on a per-particle and per-axis level, where the axes
are the Cartesian axes of the particle in its body-fixed frame.
It is important to note that starting from version 4.0 and unlike
in earlier versions of ESPResSo, the particles’ rotation is disabled by default.
In this way, just compiling in the ROTATION feature no longer changes the physics of the system.
The rotation of a particle is controlled via the
rotation property.
E.g., the following code adds a particle with rotation enabled around the x-axis of its body frame:
import espressomd
system = espressomd.System(box_l=[1, 1, 1])
system.part.add(pos=(0, 0, 0), rotation=(True, False, False))
The rotational state of a particle is stored as a quaternion in the
quat property.
For a value of (1,0,0,0), the body and space frames coincide.
When setting up a particle, its orientation state is by default aligned with the space frame of the box.
If your particles have a rotational symmetry, you can set up the particle direction
(the symmetry axis) using the director property.
Note that then you have no control over the initial rotation angle around the symmetry axis.
If your particles are anisotropic in all three directions, you can either set
the quat attribute directly,
or (recommended) set up all particle properties in the box frame and then use
rotate to rotate the particle
to the desired state before starting the simulation.
Notes:
The space-frame direction of the particle’s z-axis in its body frame is accessible through the
directorproperty.Any other vector can be converted from body to space fixed frame using the
ParticleHandle.convert_vector_body_to_space()method.When
DIPOLESare compiled in, the particles dipole moment is always co-aligned with the z-axis in the body-fixed frame.Changing the particles dipole moment and director will re-orient the particle such that its z-axis in space frame is aligned parallel to the given vector. No guarantees are made for the other two axes after setting the director or the dipole moment.
The following particle properties are related to rotation:
5.9. Virtual sites¶
Virtual sites are particles, the positions and velocities of which are not obtained by integrating an equation of motion. Rather, their coordinates are obtained from the position (and orientation) of one or more other particles. In this way, rigid arrangements of particles can be constructed and a particle can be placed in the center of mass of a set of other particles. Virtual sites can interact with other particles in the system by means of interactions. Forces are added to them according to their respective particle type. Before the next integration step, the forces accumulated on a virtual site are distributed back to those particles, from which the virtual site was derived.
There are different schemes for virtual sites, described in the following sections. The scheme acting on a virtual site is dependent on its propagation mode.
5.9.1. Rigid arrangements of particles¶
The relative implementation of virtual sites allows for the simulation of rigid arrangements of particles. It can be used, for extended dipoles and raspberry-particles, but also for more complex configurations. Position and velocity of a virtual site are obtained from the position and orientation of exactly one non-virtual particle, which has to be placed in the center of mass of the rigid body. Several virtual sites can be related to one and the same non-virtual particle. The position of the virtual site is given by
where \(\vec{x_n}\) is the position of the non-virtual particle, \(O_n\) is the orientation of the non-virtual particle, \(O_v\) denotes the orientation of the vector \(\vec{x_v}-\vec{x_n}\) with respect to the non-virtual particles body fixed frame and \(d\) the distance between virtual and non-virtual particle. In words: The virtual site is placed at a fixed distance from the non-virtual particle. When the non-virtual particle rotates, the virtual sites rotates on an orbit around the non-virtual particles center.
To use this implementation of virtual sites, activate the feature
VIRTUAL_SITES_RELATIVE. Furthermore, particles have to be set up with the
propagation modes TRANS_VS_RELATIVE
and ROT_VS_RELATIVE.
Place the particle to which the virtual site should be related. It needs to be in the center of mass of the rigid arrangement of particles you create:
import espressomd system = espressomd.System(box_l=[10., 10., 10.]) p1 = system.part.add(pos=[1., 2., 3.])
Place a particle at the desired relative position, make it virtual and relate it to the first particle:
rel_offset = [1., 0., 0.] p2 = system.part.add(pos=p1.pos + rel_offset) p2.vs_auto_relate_to(p1)
The
is_virtual()method on particlep2will now returnTrue.Repeat the previous step with more virtual sites, if desired.
To update the positions of all virtual sites, call:
system.integrator.run(0, recalc_forces=True)
Please note:
The relative position of the virtual site is defined by its distance from the non-virtual particle, the id of the non-virtual particle and a quaternion which defines the vector from non-virtual particle to virtual site in the non-virtual particles body-fixed frame. This information is saved in the virtual site’s
vs_relativeattribute. Take care, not to overwrite it after usingvs_auto_relate.Virtual sites can not be placed relative to other virtual sites, as the order in which the positions of virtual sites are updated is not guaranteed. Always relate a virtual site to a non-virtual particle placed in the center of mass of the rigid arrangement of particles.
In case you know the correct quaternions, you can also setup a virtual site using its
vs_relativeandvirtualattributes.In a simulation on more than one CPU, the effective cell size needs to be larger than the largest distance between a non-virtual particle and its associated virtual sites. To this aim, when running on more than one core, you need to set the system’s
min_global_cutattribute to this largest distance. An error is generated when this requirement is not met. Under very specific circumstances it may be desirable to disable this check, e.g. when using certain setups with the hybrid decomposition scheme. You can do so by setting the virtual sites propertyoverride_cutoff_check = True. However, only consider this if you are absolutely sure of what you are doing.If the virtual sites represent actual particles carrying a mass, the inertia tensor of the non-virtual particle in the center of mass needs to be adapted.
The presence of rigid bodies constructed by means of virtual sites adds a contribution to the scalar pressure and pressure tensor.
5.9.2. Inertialess lattice-Boltzmann tracers¶
Using the propagation mode TRANS_LB_TRACER,
the virtual sites follow the motion of a LB fluid. This is achieved by integrating
their position using the fluid velocity at the virtual sites’ position.
Forces acting on the virtual sites are directly transferred as force density
onto the lattice-Boltzmann fluid, making the coupling free of inertia.
Please note that the velocity attribute of the virtual particles
does not carry valid information for this virtual sites scheme.
The feature stems from the implementation of the
Immersed Boundary Method for soft elastic objects, but can be used independently.
5.10. Interacting with groups of particles¶
Groups of particles are addressed using ParticleSlice objects.
The objects behave similarly to ParticleList objects.
There are several ways to retrieve a particle slice:
By calling
ParticleList.add()When adding several particles at once, a particle slice is returned instead of a particle handle.
By calling
ParticleList.by_ids()It is also possible to get a slice containing particles of specific ids, e.g.:
system.part.by_ids([1, 4, 3])
would contain the particles with ids 1, 4, and 3 in that specific order.
By calling
ParticleList.all()You can get a slice containing all particles using:
system.part.all()
By calling
ParticleList.select()This is useful to filter out particles with distinct properties, e.g.:
slice1 = system.part.select(type=0, q=1) slice2 = system.part.select(lambda p: p.pos[0] < 0.5)
Properties of particle slices can be accessed just like with single particles. A list of all values is returned:
print(system.part.all().q)
A particle slice can be iterated over, see Iterating over particles and pairs of particles.
Setting properties of slices can be done by
supplying a single value that is assigned to each entry of the slice, e.g.:
system.part.by_ids(range(10)).ext_force = [1, 0, 0]
supplying an array of values that matches the length of the slice which sets each entry individually, e.g.:
system.part.by_ids(range(3)).ext_force = [[1, 0, 0], [2, 0, 0], [3, 0, 0]]
For list properties that have no fixed length like exclusions or bonds, some care has to be taken.
There, single value assignment also accepts lists/tuples just like setting the property of an individual particle. For example:
system.part.by_id(0).exclusions = [1, 2]
would both exclude short-range interactions of the particle pairs 0 <-> 1 and 0 <-> 2.
Similarly, a list can also be assigned to each entry of the slice:
system.part.by_ids(range(2,4)).exclusions = [0, 1]
This would exclude interactions between 2 <-> 0, 2 <-> 1, 3 <-> 0 and 3 <-> 1.
Now when it is desired to supply an array of values with individual values for each slice entry, the distinction can no longer be done
by the length of the input, as slice length and input length can be equal. Here, the nesting level of the input is the distinctive criterion:
system.part.by_ids(range(2,4)).exclusions = [[0, 1], [0, 1]]
The above code snippet would lead to the same exclusions as the one before.
The same accounts for the bonds property by interchanging the integer entries of the exclusion list with
the tuple (bond, partners).
You can select a subset of particles via using the select method. For example you can obtain a list of particles with charge -1 via using
system.part.select(q=-1)
For further information on how to use selections see espressomd.particle_data.ParticleList.select().
5.11. Create particular particle configurations¶
5.11.1. Setting up polymer chains¶
If you want to have polymers in your system, you can use the function
espressomd.polymer.linear_polymer_positions() to determine suitable positions.
Required arguments are the desired number of polymers n_polymers, the
number of monomers per polymer chain beads_per_chain, and the parameter
bond_length, which determines the distance between adjacent monomers
within the polymer chains.
Determining suitable particle positions pseudo-randomly requires the use of
a pseudo-random number generator, which has to be seeded. This seed
is therefore also a mandatory parameter.
The function espressomd.polymer.linear_polymer_positions() returns a
three-dimensional numpy array, namely a list of polymers containing the
positions of monomers (x, y, z). A quick example of how to set up polymers:
import espressomd
import espressomd.polymer
import espressomd.interactions
system = espressomd.System([50, 50, 50])
fene = espressomd.interactions.FeneBond(k=10, d_r_max=2)
system.bonded_inter.add(fene)
polymer_positions = espressomd.polymer.linear_polymer_positions(
n_polymers=10, beads_per_chain=25, bond_length=0.9, seed=23)
for positions in polymer_positions:
monomers = system.part.add(pos=positions)
previous_part = None
for part in monomers:
if not previous_part is None:
part.add_bond((fene, previous_part))
previous_part = part
If there are constraints present in your system which you want to be taken
into account when creating the polymer positions, you can set the optional
boolean parameter respect_constraint=True.
To simulate excluded volume while drawing the polymer positions, a minimum
distance between all particles can be set via min_distance. This will
also respect already existing particles in the system.
Both when setting respect_constraints and choosing a min_distance
trial positions are pseudo-randomly chosen and only accepted if the
requested requirement is fulfilled. Otherwise, a new attempt will be made,
up to max_tries times per monomer and if this fails max_tries per
polymer. The default value is max_tries=1000. Depending on the total
number of beads and constraints, this value may need to be adapted. If
determining suitable polymer positions within this limit fails, a runtime
error is thrown.
Note that the distance between adjacent monomers during the course of the simulation depends on the applied potentials. For fixed bond length please refer to the Rattle Shake algorithm[Andersen, 1983]. The algorithm is based on Verlet algorithm and satisfy internal constraints for molecular models with internal constraints, using Lagrange multipliers.
5.11.2. Setting up diamond polymer networks¶
espressomd.polymer.setup_diamond_polymer() creates a diamond-structured
polymer network with 8 tetra-functional nodes
connected by \(2 \times 8\) polymer chains of length MPC with the system box as
the unit cell. The box therefore has to be cubic.
The diamond command creates 16*MPC+8 many particles
which are connected via the provided bond type (the term plus 8 stems from adding 8 nodes which are connecting the chains).
Chain monomers are placed at constant distance to each other
along the vector connecting network nodes. The distance between monomers is
system.box_l[0]*(0.25 * sqrt(3))/(MPC + 1), which should be taken into account
when choosing the connecting bond.
The starting particle id, the charges of monomers, the frequency
of charged monomers in the chains as well as the types of the node particles,
the charged and the uncharged chain particles can be set via keyword arguments, see espressomd.polymer.setup_diamond_polymer().
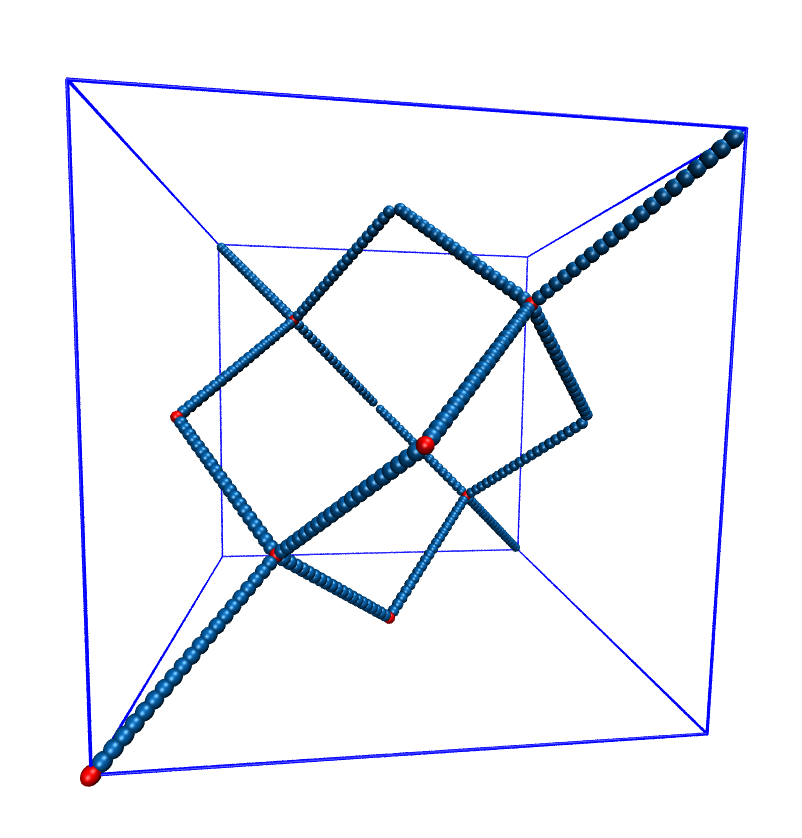
Diamond-like polymer network with MPC=15.¶
For simulating compressed or stretched gels, the function
espressomd.system.System.change_volume_and_rescale_particles() may be used.
5.12. Particle number counting feature¶
Note
Do not use these methods with the espressomd.collision_detection
module since the collision detection may create or delete particles
without the particle number counting feature being aware of this.
Therefore the espressomd.reaction_methods module may not
be used with the collision detection.
Knowing the number of particles of a certain type in simulations where particle numbers can fluctuate is of interest. Particle ids can be stored in a map for each individual type:
import espressomd
system = espressomd.System(box_l=[1, 1, 1])
system.setup_type_map([_type])
system.number_of_particles(_type)
If you want to keep track of particle ids of a certain type you have to initialize the method by calling
system.setup_type_map([_type])
After that the system will keep track of particle ids of that type. Keeping
track of particles of a given type is not enabled by default since it requires
memory. The keyword number_of_particles as argument will return the number
of particles which have the given type. For counting the number of particles
of a given type you could also use
ParticleList.select()
import espressomd
system = espressomd.System(box_l=[1, 1, 1])
system.part.add(pos=[1, 0, 0], type=0)
system.part.add(pos=[0, 1, 0], type=0)
system.part.add(pos=[0, 0, 1], type=2)
print(len(system.part.select(type=0)))
print(len(system.part.select(type=2)))
However calling select(type=type) results in looping over all particles,
which is slow. In contrast, the system
number_of_particles() method can return the
number of particles with that type.
5.13. Self-propelled swimmers¶
Note
If you are using this feature, please cite [de Graaf et al., 2016].
See also
5.13.1. Langevin swimmers¶
Note
Requires feature ENGINE.
import espressomd
system = espressomd.System(box_l=[1, 1, 1])
system.part.add(pos=[1, 0, 0], swimming={'f_swim': 0.03})
This enables the particle to be self-propelled along its director.
The terminal propulsion speed is determined by the friction of a (Langevin)
thermostat (v_swim = f_swim / gamma).
5.13.2. Lattice-Boltzmann swimmers¶
Note
Requires features ENGINE and VIRTUAL_SITES_RELATIVE.
import espressomd
system = espressomd.System(box_l=[1, 1, 1])
swimmer = system.part.add(pos=[2, 0, 0],
rotation=[True, True, True],
swimming={'f_swim': 0.01})
In lattice-Boltzmann, self-propulsion is less trivial than for regular MD, because for hydrodynamic interactions it is important that the propulsion force is generated by the swimmer itself and not by an external force. Since the swimmer can only push itself forward by pushing fluid backward, the total system is net force-free at all times. The resulting flow-field can thus not contain monopolar contributions in the far field and the slowest-decaying flow-field mode is a dipole. In ESPResSo, the propulsion mechanism can be mimicked by applying a force to the fluid that is equal in magnitude but opposite in sign to the forward force on the swimming particle. For this, particles can be marked as force appliers as shown in the following example:
dipole = system.part.add(pos=[1, 0, 0],
swimming={"f_swim": swimmer.swimming["f_swim"],
"is_engine_force_on_fluid": True})
dipole.vs_auto_relate_to(swimmer)
dipole.vs_quat = calc_quaternions_from_angles(np.pi, 0.)
This makes the dipole particle not experience any friction or stochastic forces,
but apply f_swim along its internal orientation (director)
and follow the swimmer while updating its orientation accordingly.
ESPResSo provides a helper function add_dipole_particle() to set
up the virtual particle with the correct distance, relative position and orientation:
import espressomd.swimmer_helpers.add_dipole_particle as add_dip
dipole = add_dip(system, swimmer, 2., 0, mode="pusher")
It creates pushers with the propulsion behind the swimmer and pullers with the propulsion in front of the swimmer.
Notes:
The terminal velocity is not
v_swim = gamma_lb * f_swim. The flow-field generated by the dipole particle interacts in a non-trivial way with the swimmer particle. You will have to calibrate your propulsion force to the desired swim velocity.For the same reason, do not place the dipole particle too close to the swimmer (at least one grid spacing is recommended). Lattice-Boltzmann cannot create an exact, mathematical dipole, which would require zero distance but diverging forces.
Since the swimmer is a point particle, it cannot experience shear or rotational flow components, only random rotational noise. If shear or rotational flow are important in your system, consider creating an extended, raspberry particle as described in Rigid arrangements of particles.